Unlocking the Power of 3-Phase Systems: Understanding Phasor Diagrams
Ever wondered how electricity gets delivered to your home or powers those massive industrial machines? A key player in this process is the three-phase power system, a more efficient and powerful way of transmitting electricity compared to single-phase systems. But how do we visualize and understand the complex interactions within these systems? Enter the phasor diagram, a powerful tool that simplifies the analysis of three-phase systems.
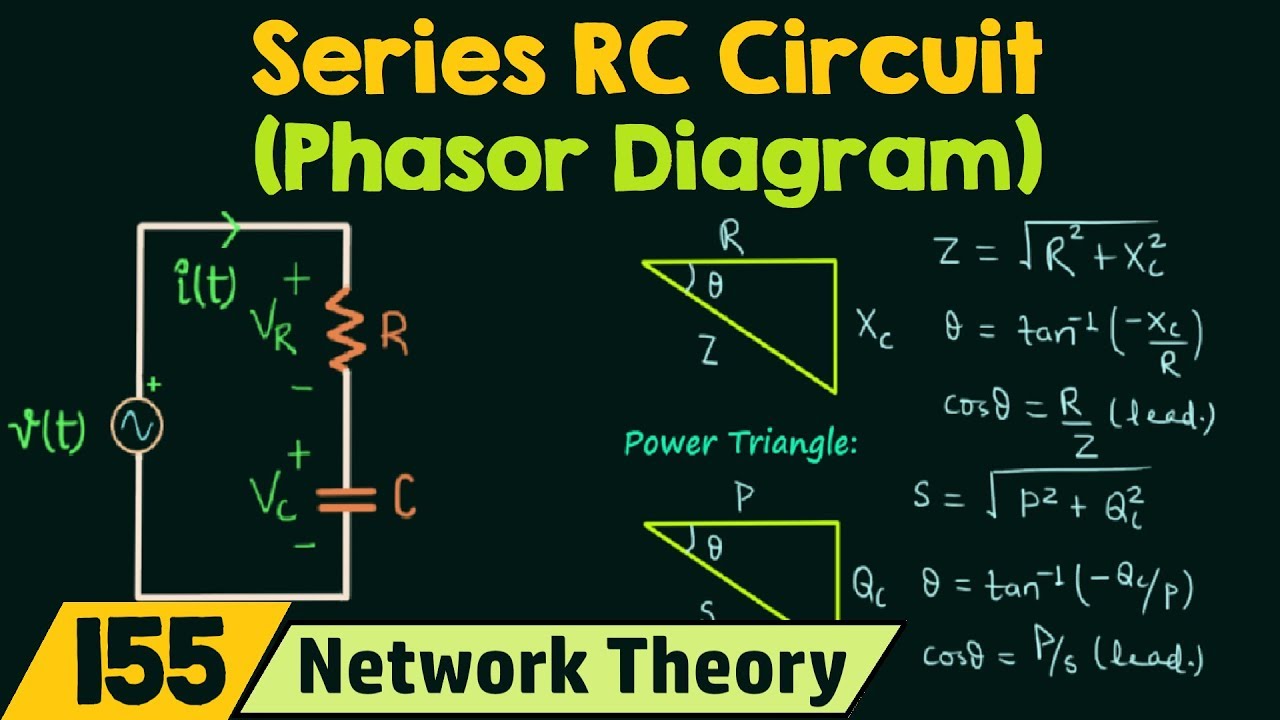
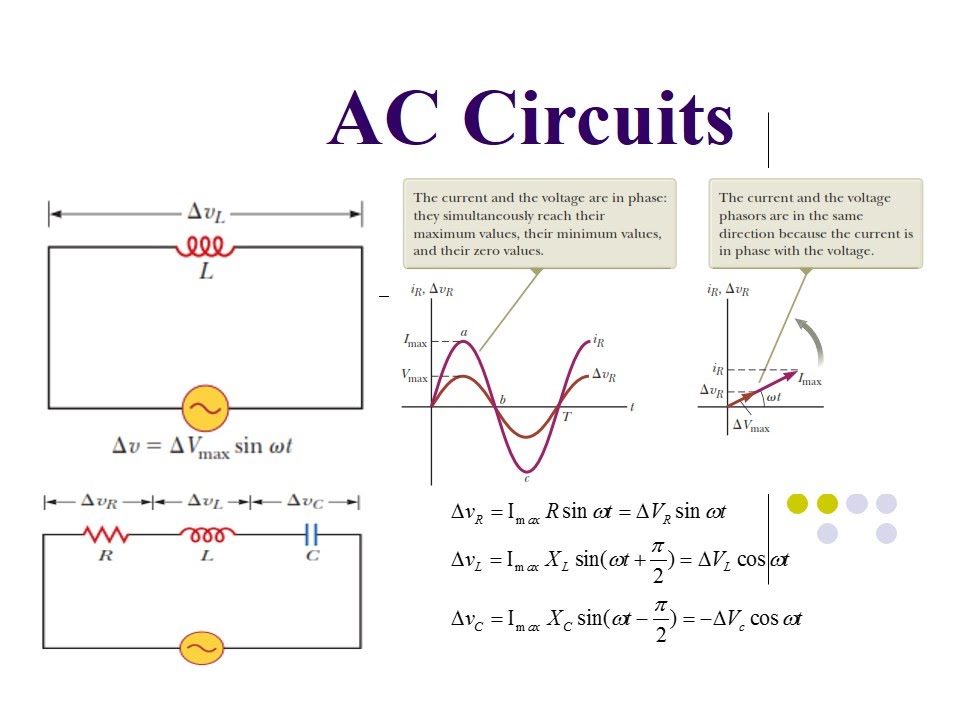
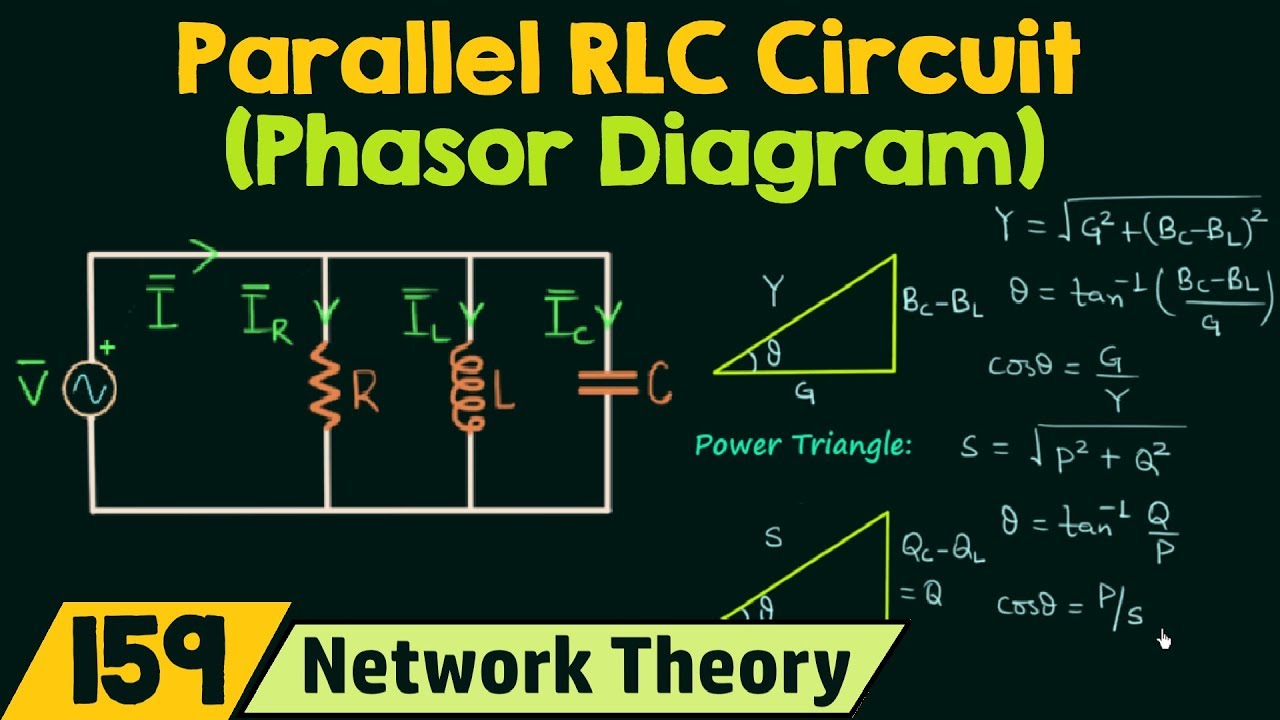
Phasor diagrams provide a visual representation of the magnitude and phase relationships between voltages and currents in AC circuits, particularly useful in three-phase systems where multiple sinusoidal waveforms interact. These diagrams transform complex mathematical equations into easily understandable graphical representations, enabling engineers to quickly grasp the system's behavior. Understanding these diagrams is essential for anyone working with electrical power systems, from design engineers to technicians.
The concept of representing sinusoidal quantities with rotating vectors, or phasors, originated with Charles Proteus Steinmetz in the late 19th century. His work revolutionized AC circuit analysis, providing a more intuitive method than complex calculus. The application of phasor diagrams to three-phase systems became crucial with the widespread adoption of these systems for power generation and distribution in the early 20th century. The ability to visualize phase differences and voltage/current relationships became essential for designing efficient and stable power grids.
The importance of understanding three-phase phasor diagrams cannot be overstated. They are crucial for analyzing power flow, calculating fault currents, and designing protective relaying schemes. Misinterpreting or neglecting these diagrams can lead to costly errors in system design, potentially resulting in instability, equipment damage, or even power outages. Therefore, a thorough grasp of phasor representation is fundamental for anyone involved in the design, operation, or maintenance of three-phase power systems.
Imagine three sinusoidal waves, slightly offset from each other in time. These represent the voltages in a three-phase system. A phasor diagram for a balanced three-phase system depicts these voltages as three vectors of equal magnitude, separated by 120 degrees. This visual representation instantly conveys the phase relationship between the voltages, simplifying complex calculations involving sinusoidal functions. This graphical approach provides invaluable insights into the system's behavior.
One of the key benefits of using phasor diagrams is the simplification of complex calculations. Instead of dealing with trigonometric functions, engineers can use vector addition and subtraction to analyze circuit behavior. This makes analyzing unbalanced systems or calculating fault currents considerably easier. Furthermore, visualizing the phase relationships allows for a quicker understanding of power flow and system stability.
Another advantage is the ability to easily visualize the impact of system changes. For instance, adding a load to one phase can be represented by modifying the corresponding phasor on the diagram, allowing engineers to quickly assess the impact on the overall system balance. This visual representation aids in troubleshooting and optimizing system performance.
Lastly, phasor diagrams facilitate the understanding of complex concepts like power factor and reactive power. These concepts, often difficult to grasp through equations alone, become more intuitive when visualized on a phasor diagram. This improved understanding is crucial for designing efficient power systems.
Advantages and Disadvantages of Using Phasor Diagrams
| Advantages | Disadvantages |
|---|---|
| Simplifies complex calculations | Limited to steady-state analysis |
| Visualizes phase relationships | Can be complex for highly unbalanced systems |
| Facilitates understanding of power factor and reactive power | Requires basic understanding of vector algebra |
Frequently Asked Questions:
1. What is a phasor? - A phasor is a rotating vector representing a sinusoidal quantity.
2. Why are phasor diagrams used in three-phase systems? - They simplify the analysis of voltage and current relationships.
3. What is a balanced three-phase system? - A system where all three phases have equal magnitude and 120-degree phase difference.
4. How are unbalanced systems represented on a phasor diagram? - The phasors will have different magnitudes or unequal phase angles.
5. What is the significance of the angle between phasors? - It represents the phase difference between the corresponding sinusoidal quantities.
6. How can phasor diagrams help in fault analysis? - They help visualize the magnitude and direction of fault currents.
7. What is the relationship between phasor diagrams and power factor? - The angle between voltage and current phasors is related to the power factor.
8. Where can I learn more about phasor diagrams? - Textbooks on electrical circuits and online resources provide detailed information.
In conclusion, the phasor diagram is an invaluable tool for understanding and analyzing three-phase power systems. Its ability to simplify complex calculations and visualize phase relationships makes it essential for engineers and technicians. From designing efficient power grids to troubleshooting faults, understanding phasor diagrams empowers professionals to effectively manage and optimize these complex systems. By mastering this powerful technique, you gain a deeper understanding of the very foundation of modern power distribution and unlock the full potential of three-phase power systems. Dive into the world of phasor diagrams and empower yourself with the knowledge to tackle the challenges and opportunities of the electrical world.
Afc ann arbor decoding the mighty oaks fixture list
How to save instagram profile pictures a complete guide
Unlocking fluency your guide to mastering hari kerja workdays in indonesian