Taming the Electrical Wild West: Understanding AC Circuit Phasors
Ever feel like alternating current (AC) circuits are a total enigma, a swirling vortex of voltage and current that's impossible to grasp? Like, how do you even *begin* to analyze these constantly fluctuating signals? Enter the phasor, your trusty compass in the wild west of electrical engineering. This elegant tool transforms complex sinusoidal waves into manageable vectors, making AC circuit analysis significantly less daunting.
Imagine trying to track the position of a spinning carousel horse. Its height constantly changes as it goes up and down, making it tricky to pinpoint its exact location. A phasor representation of this motion would be a single arrow, rotating like the carousel, whose length represents the horse's maximum height. This arrow, the phasor, captures the essence of the cyclical motion without getting bogged down in the constantly changing instantaneous values. Similarly, phasor analysis provides a simplified way to represent sinusoidal voltages and currents in AC circuits.
The birth of phasor analysis can be traced back to the late 19th century with the rise of AC power systems. Charles Proteus Steinmetz, a brilliant mathematician and electrical engineer, is credited with popularizing the use of complex numbers and phasors in AC circuit analysis. Before phasors, analyzing AC circuits involving inductors and capacitors was a headache-inducing process requiring complicated differential equations. Phasors revolutionized the field, providing a visually intuitive and mathematically simpler method.
The importance of phasor analysis in modern electrical engineering cannot be overstated. It's the bedrock of power system analysis, used in designing everything from power grids to electric motors. Without phasors, understanding and predicting the behavior of AC circuits – which power our homes, industries, and practically everything around us – would be incredibly difficult.
Phasors address the fundamental issue of analyzing sinusoidal signals that constantly change in magnitude and direction. By representing these signals as rotating vectors, we can effectively "freeze" the sinusoidal variations at a specific point in time and analyze the circuit's steady-state behavior. This simplification is akin to taking a snapshot of the spinning carousel horse; the snapshot doesn't capture the motion, but it provides crucial information about the horse's maximum height and its position at a specific instant.
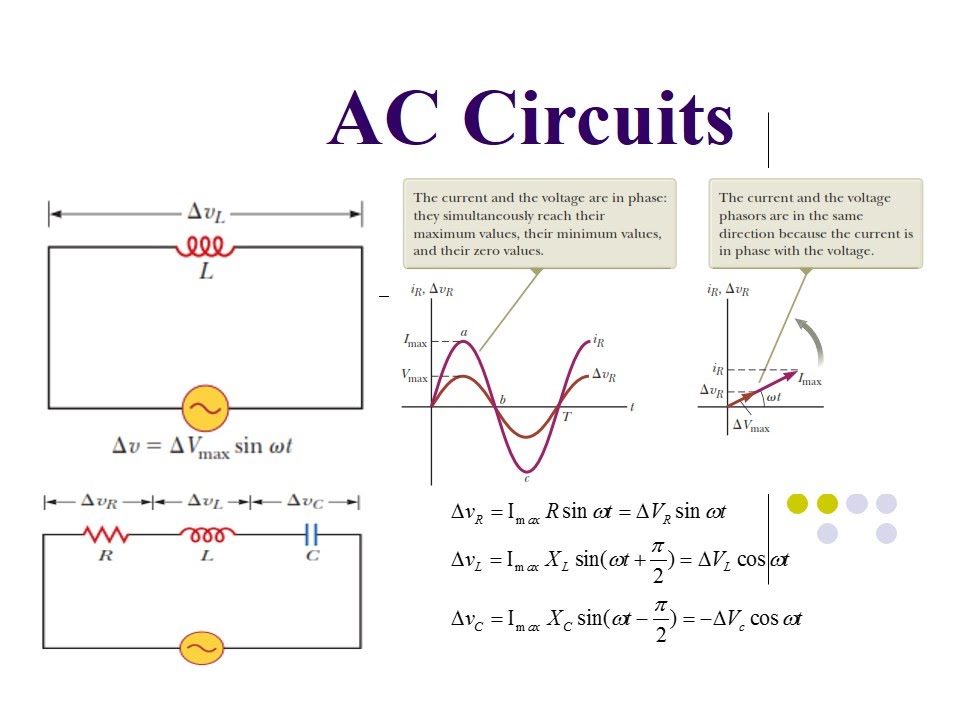
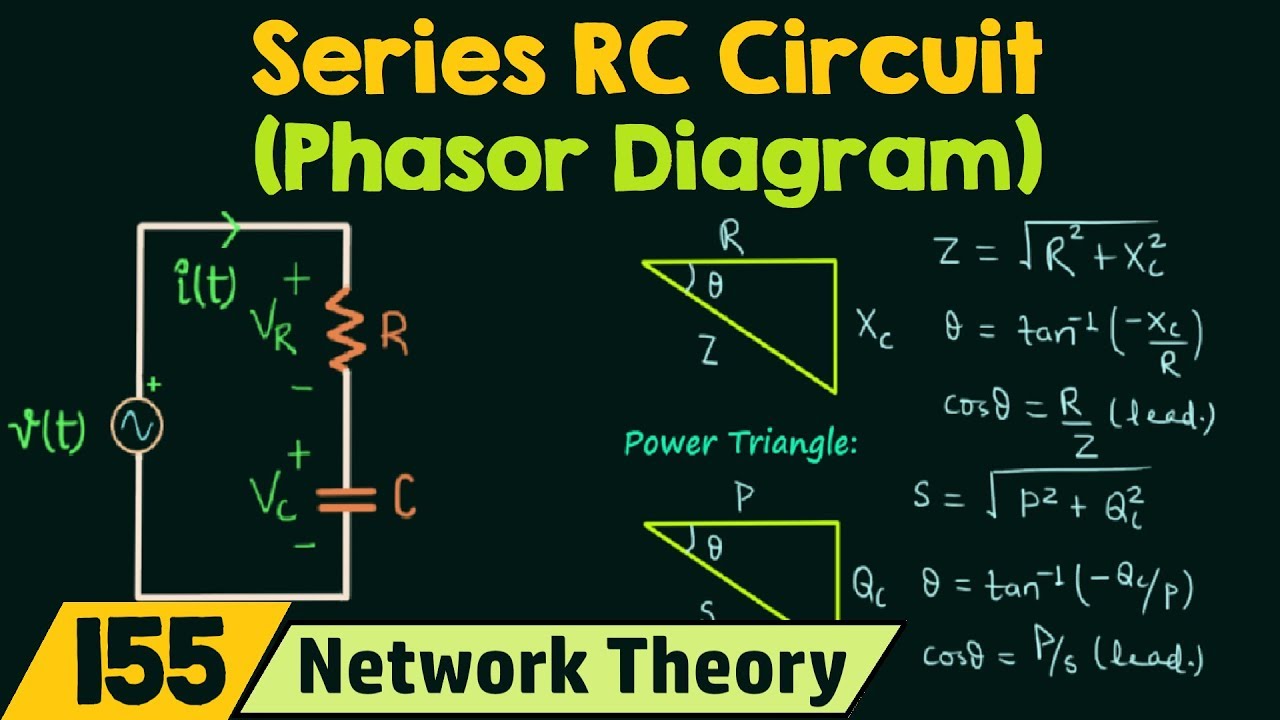
A phasor is a complex number representing the amplitude and phase of a sinusoidal function. It's essentially a rotating vector in the complex plane. The length of the vector corresponds to the amplitude of the sinusoid, and the angle it makes with the horizontal axis represents the phase shift. For example, a voltage signal described by v(t) = Vmax*cos(ωt + φ) is represented by the phasor V = Vmax∠φ.
One key benefit of using phasors is simplification of AC circuit calculations. Instead of dealing with trigonometric functions and differential equations, we can use basic algebra and complex number arithmetic. This makes analyzing complex circuits with multiple components much easier.
Another advantage is the visualization aspect. Phasor diagrams provide a clear graphical representation of the relationships between voltages and currents in a circuit. This makes it easier to understand the circuit's behavior and identify potential problems.
Furthermore, phasors are indispensable for power system analysis, enabling engineers to analyze the flow of power in large networks and ensure stability and reliability.
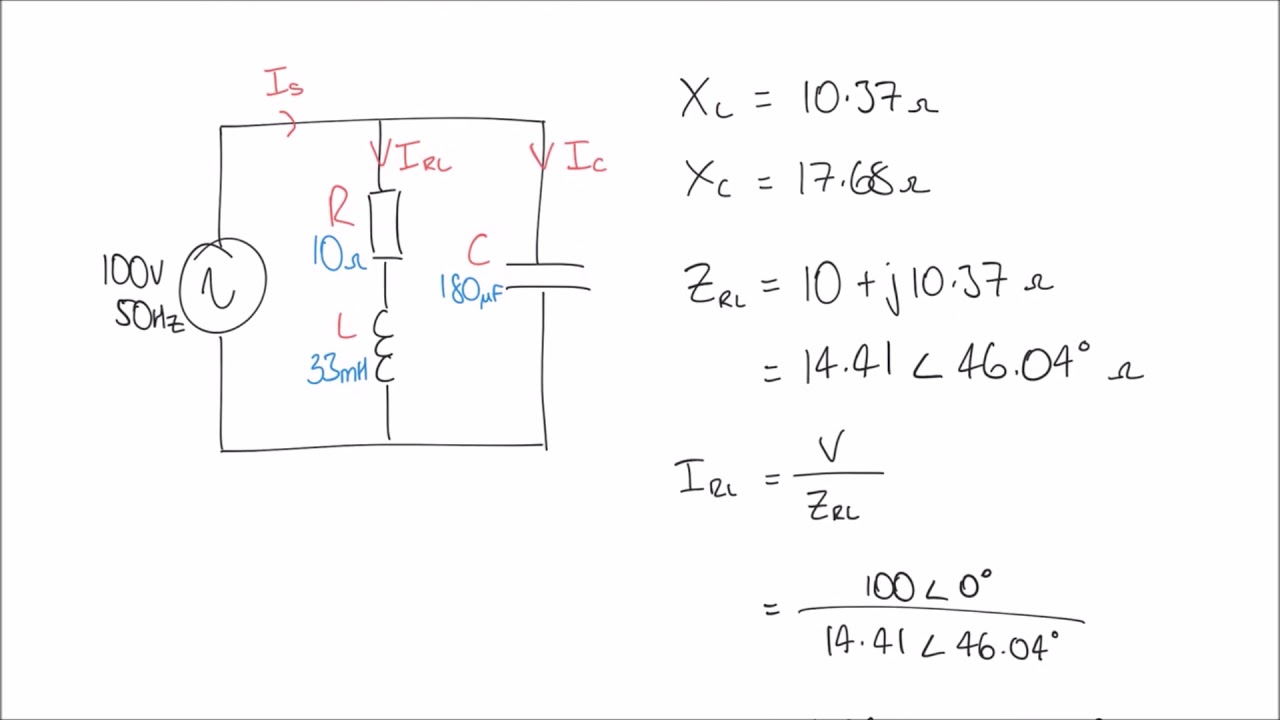
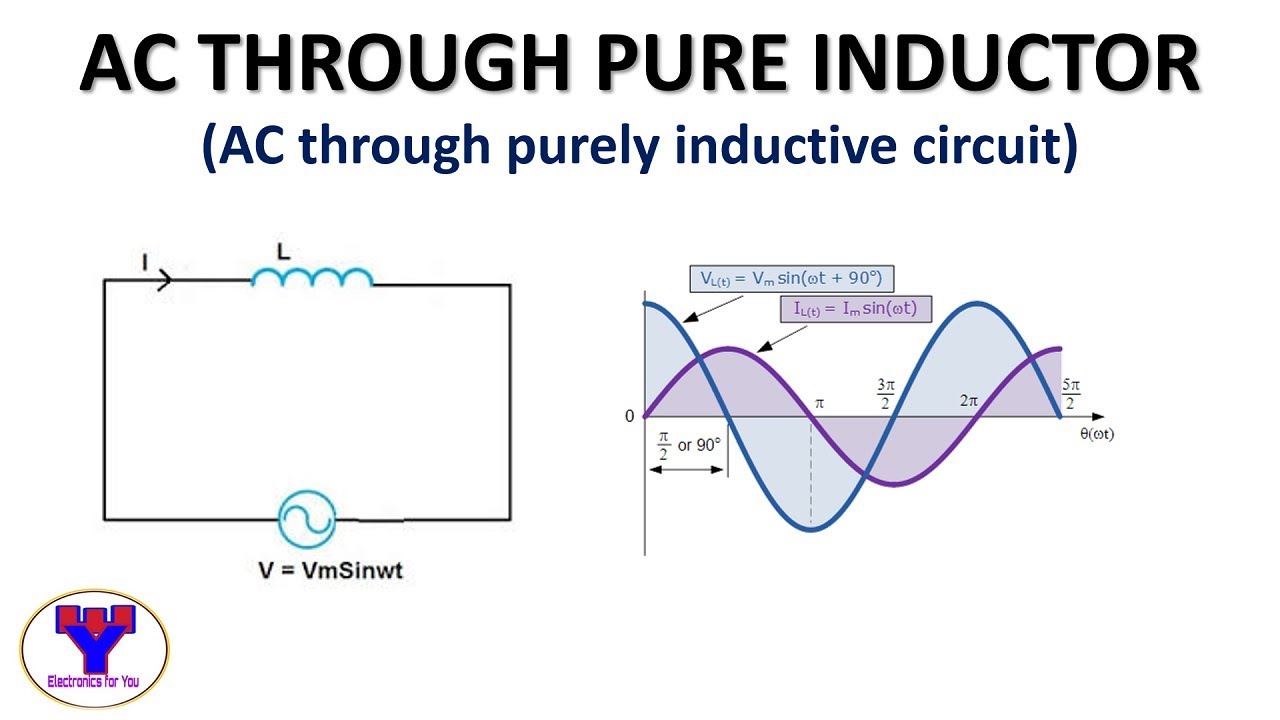
In AC circuit analysis with phasors, a resistor's impedance is simply its resistance. For an inductor, the impedance is jωL, and for a capacitor, it's 1/jωC. Here, j represents the imaginary unit, ω is the angular frequency, L is the inductance, and C is the capacitance.
Advantages and Disadvantages of Phasor Analysis
| Advantages | Disadvantages |
|---|---|
| Simplifies AC circuit calculations | Only applicable to sinusoidal steady-state analysis |
| Provides visual representation through phasor diagrams | Doesn't capture transient behavior |
| Essential for power system analysis | Requires understanding of complex numbers |
Frequently Asked Questions: What is a phasor? How do you convert a sinusoidal function to a phasor? What is the impedance of an inductor or capacitor in phasor form? How do you use phasors to analyze series and parallel circuits? What is the concept of phasor diagrams? How are phasors used in power system analysis? What are the limitations of phasor analysis? What are some real-world applications of phasors?
One tip for working with phasors is to always remember that they represent sinusoidal signals at a specific frequency. Don't mix phasors representing signals at different frequencies.
In conclusion, phasor analysis is a cornerstone of electrical engineering, providing a powerful and elegant way to analyze AC circuits. It transforms complex sinusoidal functions into manageable vectors, simplifying calculations and offering valuable visual insights into circuit behavior. From designing power grids to understanding the intricacies of electronic devices, phasors are essential tools for any electrical engineer. Embrace the power of phasors and conquer the electrical wild west! By mastering this technique, you’ll unlock a deeper understanding of AC circuits and pave the way for exciting explorations in the world of electrical engineering. So, grab your metaphorical compass (your understanding of phasors) and navigate the electrifying landscape of AC circuits with confidence!
Small tub for small bathroom big relaxation in a tiny space
Unlocking the secrets of plantation au jardin avec la lune
The duality of charm blonde and black hair guy anime