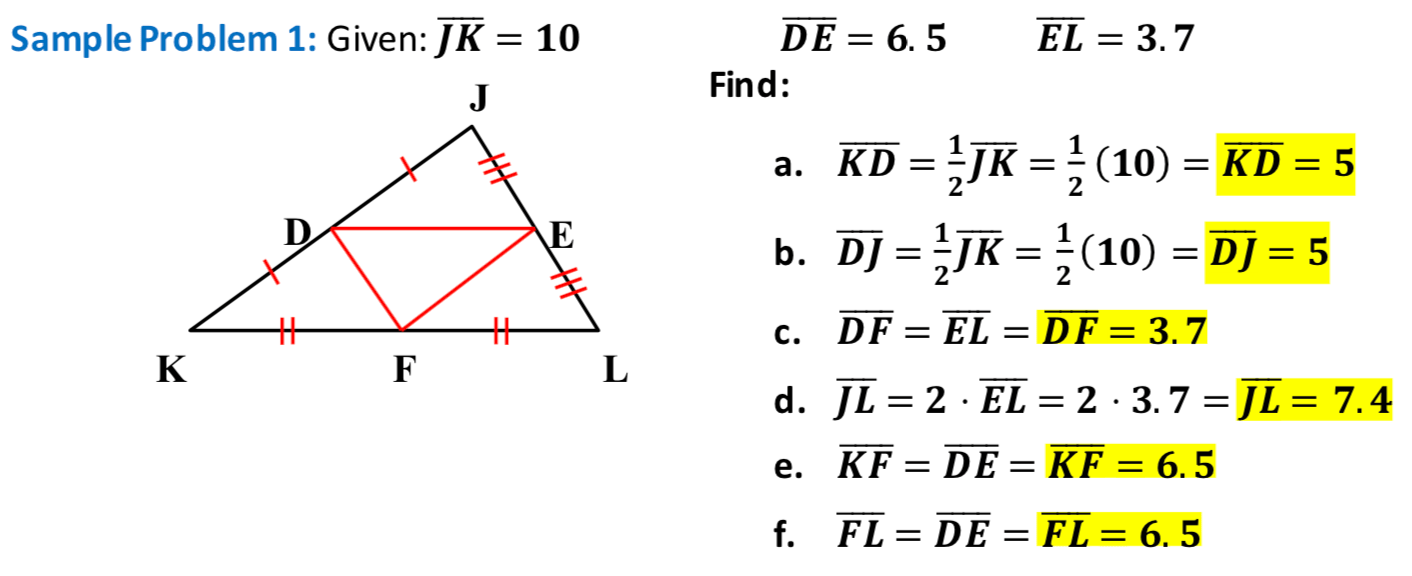Midsegments Of Triangles Formula
Triangles are a fundamental shape in geometry, with various properties and characteristics that have puzzled and fascinated mathematicians for centuries. One of the intriguing aspects of triangles is the concept of midsegments, which play a crucial role in understanding the structure and properties of these geometric shapes. In this article, we will delve into the fascinating world of midsegments of triangles and explore their formula, significance, benefits, and practical applications.
History, Origin, Importance of Midsegments of Triangles Formula
The midsegments of triangles formula has been studied and utilized by mathematicians for centuries, dating back to ancient civilizations such as the Greeks and Egyptians. These midsegments play a vital role in dissecting triangles into smaller, more manageable parts, providing insights into their properties and relationships. Understanding the formula for midsegments of triangles is essential for solving complex geometric problems and applications in various fields such as engineering, architecture, and physics.
Definition, Explanation, and Simple Examples of Midsegments of Triangles Formula
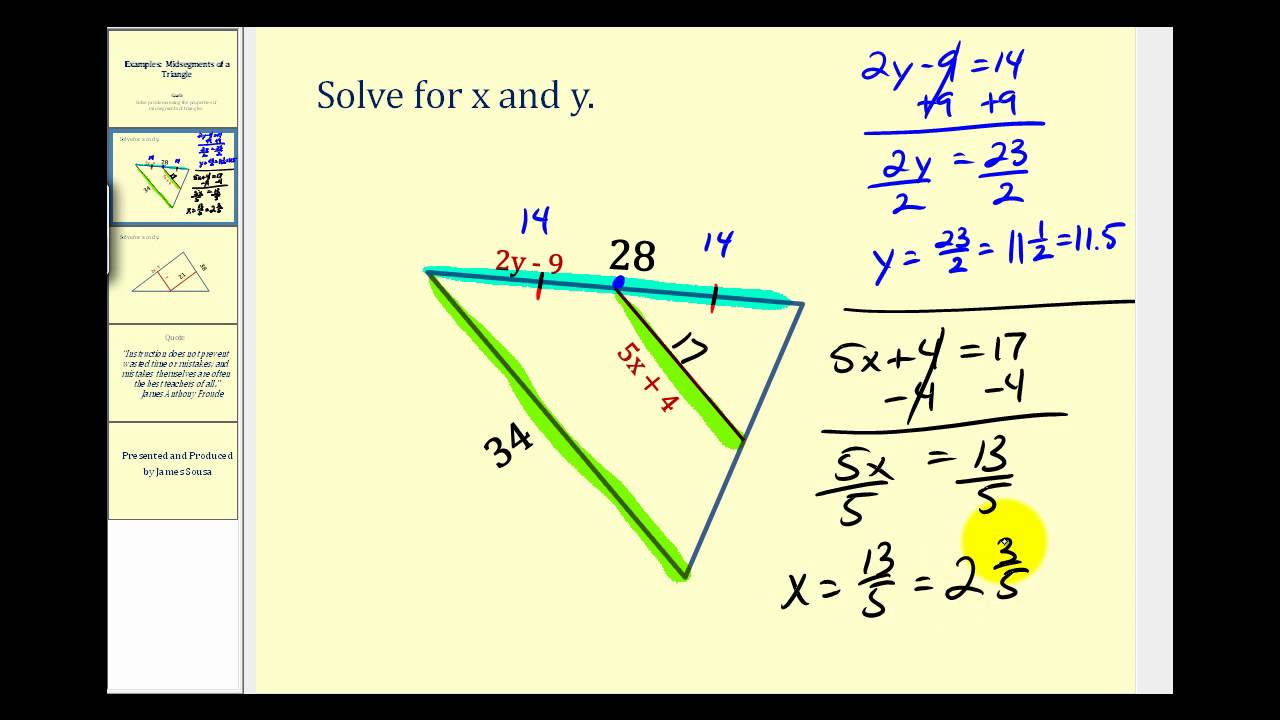
In geometry, a midsegment of a triangle is a line segment connecting the midpoints of two sides of a triangle. The formula for finding the length of a midsegment is to take the average of the lengths of the two sides it connects. For example, if a midsegment connects two sides of lengths 4 and 6, the length of the midsegment would be (4 + 6) / 2 = 5.
Benefits of Midsegments of Triangles Formula
- Simplifies Triangle Analysis: The midsegments formula simplifies the analysis of complex triangles by breaking them down into more manageable components.
- Provides Insight into Triangle Properties: By studying midsegments, we can gain a deeper understanding of the relationships and properties of triangles.
- Facilitates Problem Solving: The midsegments formula serves as a valuable tool for solving geometric problems efficiently and accurately.
Action Plan for Midsegments of Triangles Formula
To utilize the midsegments of triangles formula effectively, it is essential to follow a systematic approach that includes identifying the sides, calculating the midpoints, and applying the formula to determine the length of the midsegment. By following these steps, you can analyze triangles with ease and precision.
Checklist for Midsegments of Triangles Formula
- Identify the two sides that the midsegment connects.
- Calculate the midpoints of these sides.
- Apply the formula to find the length of the midsegment.
Step-by-Step Guide on Midsegments of Triangles Formula
- Identify the lengths of the two sides the midsegment connects.
- Calculate the average of these lengths.
- The result is the length of the midsegment.
Recommendations for Resources on Midsegments of Triangles Formula
For further study and practice on midsegments of triangles formula, check out online geometry resources, textbooks on trigonometry, and educational apps on geometry. These tools can provide additional exercises and examples to enhance your understanding of the topic.
Advantages and Disadvantages of Midsegments of Triangles Formula
While the midsegments formula offers numerous advantages in solving geometric problems, some disadvantages include the need for precision in calculations and the potential for errors in measurement. However, with practice and attention to detail, these drawbacks can be minimized.
Best Practices for Implementing Midsegments of Triangles Formula
- Double-check calculations to ensure accuracy.
- Use visual aids such as diagrams to visualize the midsegments.
- Practice applying the formula to various triangle configurations for mastery.
Real-Life Examples of Midsegments of Triangles Formula
- In architecture, midsegments are used to analyze the structural stability of triangular trusses.
- In engineering, midsegments help determine the center of gravity in triangular frameworks.
- In physics, midsegments are applied in calculating the force distribution in triangular structures.
Challenges and Solutions for Midsegments of Triangles Formula
- Challenge: Precision in measurements. Solution: Use precise tools and techniques for accurate calculations.
- Challenge: Complex triangle configurations. Solution: Break down the triangle into simpler components for analysis.
- Challenge: Understanding triangle properties. Solution: Study and practice applying the midsegments formula regularly.
Questions and Answers about Midsegments of Triangles Formula
- What is a midsegment of a triangle? A midsegment is a line segment connecting the midpoints of two sides of a triangle.
- How do you calculate the length of a midsegment? The length of a midsegment is the average of the lengths of the two sides it connects.
- Why are midsegments important in geometry? Midsegments provide insights into the properties and relationships of triangles like no other geometric concept.
Tips and Tricks for Midsegments of Triangles Formula
- Use the midpoint formula to find the midpoints of the sides.
- Remember to average the lengths of the two sides to find the length of the midsegment accurately.
- Practice applying the midsegments formula to various triangle configurations for proficiency.
Conclusion: Unlocking the Secrets of Midsegments of Triangles Formula
In conclusion, the midsegments of triangles formula is an indispensable tool for understanding the intricate properties and relationships of triangles. By mastering this formula and its applications, you can unlock the secrets of geometric analysis with precision and clarity. Embrace the challenge of exploring the world of midsegments and discover the beauty and elegance of triangles in a whole new light. Take action today, apply the formula, and witness the magic of geometry unfold before your eyes.
Unlocking efficiency the power of persona sentada de frente
The allure of sudden transformation embracing unexpected beauty
The roaring twenties a glimpse into historia de los anos 20