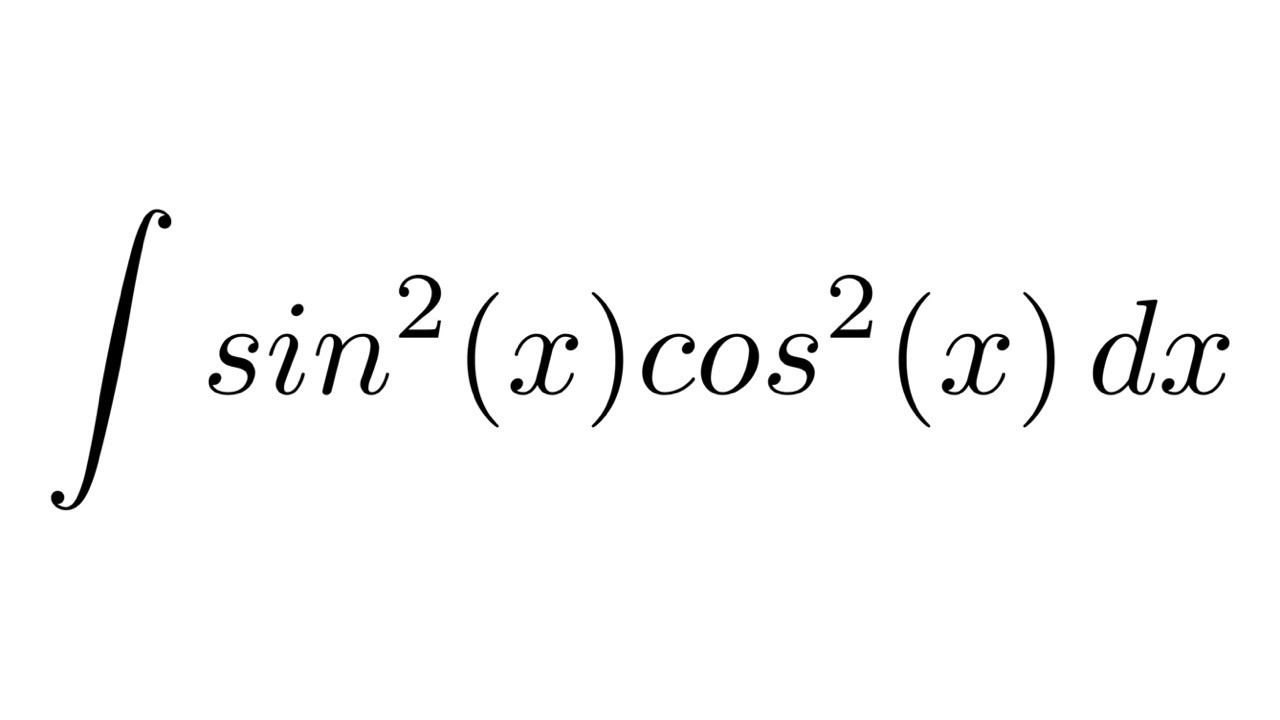Integreren van Cos 2x Sin x: Een Uitgebreide Gids
De wereld van de calculus zit vol met intrigerende uitdagingen en elegante oplossingen. Een van die uitdagingen die we vandaag onderzoeken, is het integreren van de trigonometrische uitdrukking cos 2x sin x. Hoewel het op het eerste gezicht misschien een abstracte wiskundige oefening lijkt, heeft het integreren van cos 2x sin x brede toepassingen in verschillende wetenschappelijke en technische disciplines.
Voordat we ons verdiepen in de technische details, nemen we even de tijd om de basisprincipes te begrijpen. Integratie, in wezen de inverse bewerking van differentiatie, stelt ons in staat om de oppervlakte onder een curve te vinden, wat een fundamenteel concept is in de calculus. Wanneer we te maken hebben met trigonometrische functies zoals cos 2x sin x, wordt integratie een hulpmiddel om periodieke verschijnselen in verschillende wetenschappelijke gebieden, van natuurkunde tot engineering, te modelleren en te analyseren.
De uitdrukking cos 2x sin x zelf vertegenwoordigt een product van twee trigonometrische functies, waardoor het een integraal is die een beetje strategie vereist om op te lossen. Gelukkig biedt de calculus ons een handig hulpmiddel om met dergelijke integralen om te gaan: de substitutieregel. Deze regel stelt ons in staat om een nieuwe variabele te introduceren, waardoor de integraal vaak aanzienlijk wordt vereenvoudigd.
Om de integraal van cos 2x sin x te vinden, passen we de substitutieregel toe en gebruiken we onze kennis van trigonometrische identiteiten. Het proces omvat het substitueren van een deel van de integrand door een nieuwe variabele, in dit geval u = 2x. Deze substitutie vereenvoudigt niet alleen de integraal, maar belicht ook de elegantie van de calculus bij het aanpakken van complexe wiskundige uitdrukkingen.
Na het uitvoeren van de substitutie en het toepassen van de juiste trigonometrische identiteiten, bereiken we de oplossing voor de integraal van cos 2x sin x. Deze oplossing, die meestal een nieuwe functie plus een integratieconstante omvat, vertegenwoordigt een familie van functies waarvan de afgeleide de oorspronkelijke integrand is. Het is essentieel om te onthouden dat de integratieconstante alle constante termen vertegenwoordigt die verloren zijn gegaan tijdens de differentiatie.
Voor- en nadelen van Integratietechnieken
Hoewel de substitutieregel een krachtig hulpmiddel is voor het integreren van cos 2x sin x, is het de moeite waard om de voor- en nadelen van verschillende integratietechnieken te onderzoeken:
| Techniek | Voordelen | Nadelen |
|---|---|---|
| Substitutieregel | Vereenvoudigt de integraal, effectief voor samengestelde functies | Vereist mogelijk meerdere substituties, werkt mogelijk niet voor alle integralen |
| Integratie door onderdelen | Geschikt voor producten van functies, kan worden gebruikt wanneer substitutie mislukt | Kan leiden tot complexere integralen, vereist mogelijk meerdere toepassingen |
| Partiële breuken | Effectief voor rationale functies, breekt complexe uitdrukkingen op in eenvoudigere | Vereist mogelijk gedeeltelijke breukdecompositie, werkt alleen voor rationale functies |
Beste praktijken voor het integreren van trigonometrische functies
Hier zijn enkele beste praktijken om in gedachten te houden bij het integreren van trigonometrische functies zoals cos 2x sin x:
- Vereenvoudig de integrand: gebruik trigonometrische identiteiten om de integrand indien mogelijk te vereenvoudigen voordat u met integratie begint.
- Kies de juiste techniek: bepaal de meest geschikte integratietechniek op basis van de vorm van de integrand.
- Substitutie: gebruik substitutie om de integraal te vereenvoudigen als de integrand een samengestelde functie of een trigonometrische functie met een meervoudige hoek bevat.
- Integratie door onderdelen: overweeg integratie door onderdelen wanneer de integrand een product van functies is.
- Controleer uw antwoord: differentieer uw antwoord om er zeker van te zijn dat het overeenkomt met de oorspronkelijke integrand.
Veelgestelde vragen over het integreren van Cos 2x Sin x
Hier zijn enkele veelgestelde vragen over het integreren van cos 2x sin x:
V: Wat is de integraal van cos 2x sin x?
A: De integraal van cos 2x sin x is -(1/2)cos^2(x) + C, waarbij C een integratieconstante is.
V: Hoe gebruik ik de substitutieregel om cos 2x sin x te integreren?
A: Om de substitutieregel te gebruiken, stelt u u = 2x in. Dan is du = 2 dx. Vervang deze waarden in de integraal en vereenvoudig om -(1/2) ∫ cos(u) sin(u) du te krijgen. Deze integraal kan worden opgelost met een andere substitutie (w = cos(u)).
V: Kan ik integratie door onderdelen gebruiken om cos 2x sin x te integreren?
A: Hoewel integratie door onderdelen kan worden gebruikt, is het niet de meest efficiënte methode voor deze specifieke integraal. De substitutieregel is een eenvoudigere benadering.
V: Wat zijn enkele veelvoorkomende toepassingen van het integreren van trigonometrische functies?
A: Het integreren van trigonometrische functies heeft toepassingen in de natuurkunde (bijvoorbeeld het berekenen van arbeid en energie), engineering (bijvoorbeeld het analyseren van golven en trillingen) en andere gebieden waar periodieke verschijnselen moeten worden gemodelleerd.
Conclusie
Het integreren van cos 2x sin x, hoewel het in eerste instantie een ontmoedigende taak lijkt, wordt beheersbaar met de juiste kennis van calculus en trigonometrische identiteiten. Door de kracht van de substitutieregel te benutten, kunnen we deze integraal vereenvoudigen en zijn oplossing vinden, waardoor we de elegantie en kracht van de calculus kunnen waarderen bij het aanpakken van complexe wiskundige uitdrukkingen. De reis door de wereld van de calculus is er een van voortdurende verkenning en ontdekking, en het beheersen van technieken zoals het integreren van cos 2x sin x stelt ons in staat om de taal van het universum beter te begrijpen en te waarderen.
Ontketen je innerlijke dj download een music mixer
Ll cool j greatest hits cd een reis door hiphopgeschiedenis
Communicatie zonder gedoe online talkies zonder download
