De Wondere Wereld van Vijfhoeken: Vormen, Afbeeldingen en Wiskunde
Vijfhoeken, met hun vijf gelijke zijden en vijf gelijke hoeken, bekoren ons al eeuwenlang. Van de majestueuze Pentagon-gebouw in Washington D.C. tot de delicate bloemblaadjes van een viooltje, deze fascinerende vorm duikt overal in ons leven op, vaak zonder dat we het beseffen.
Maar wat maakt vijfhoeken zo bijzonder? Het antwoord ligt in hun unieke wiskundige eigenschappen en de esthetische aantrekkingskracht die ze uitoefenen. In dit artikel duiken we in de wondere wereld van vijfhoeken, verkennen we hun geschiedenis, ontrafelen we hun geheimen en ontdekken we hun betekenis in ons dagelijks leven.
Al in de oudheid waren wiskundigen gefascineerd door de vijfhoek. De oude Grieken, met hun liefde voor geometrie, ontdekten de gulden snede – een speciale verhouding die vaak voorkomt in de natuur en die nauw verbonden is met de constructie van een regelmatige vijfhoek. Deze ontdekking opende de deur naar nieuwe inzichten in de geometrie en de wiskunde, en beïnvloedde kunst, architectuur en design door de eeuwen heen.
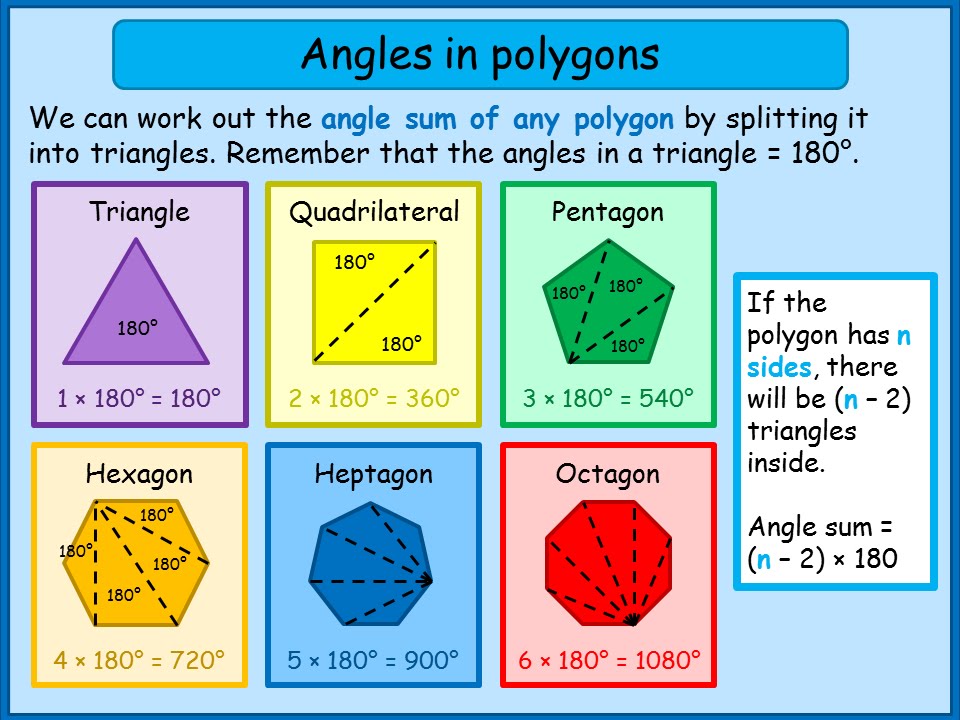
Vijfhoeken zijn niet alleen mooi om naar te kijken, ze hebben ook interessante wiskundige eigenschappen. Wist je bijvoorbeeld dat de som van de binnenhoeken van een vijfhoek altijd 540 graden is? Of dat je een perfecte vijfhoek kunt construeren met behulp van alleen een passer en een liniaal? Deze wiskundige eigenaardigheden maken vijfhoeken tot een dankbaar onderwerp voor studie en verkenning, zowel voor beginnende als gevorderde wiskundigen.
Naast hun esthetische en wiskundige waarde, hebben vijfhoeken ook praktische toepassingen. In de architectuur worden ze gebruikt om sterke en stabiele constructies te creëren. In de natuur vinden we ze terug in de vorm van bloemblaadjes, zeesterren en zelfs in de structuur van bepaalde virussen. Door de eigenschappen van vijfhoeken te bestuderen, kunnen we onze kennis van de wereld om ons heen vergroten en nieuwe technologieën ontwikkelen.
Voordelen van Vijfhoeken
Vijfhoeken bieden een aantal voordelen, waardoor ze een fascinerend onderwerp zijn voor studie en toepassing:
| Voordeel | Uitleg |
|---|---|
| Esthetische aantrekkingskracht | Vijfhoeken worden vaak gezien als een aantrekkelijke en harmonieuze vorm, die een gevoel van evenwicht en symmetrie oproept. |
| Wiskundige eigenschappen | De unieke wiskundige eigenschappen van vijfhoeken, zoals de gulden snede en de som van de binnenhoeken, maken ze interessant voor studie en onderzoek. |
| Praktische toepassingen | Vijfhoeken worden gebruikt in architectuur, natuur en technologie vanwege hun sterkte, stabiliteit en andere nuttige eigenschappen. |
Vijf Concrete Voorbeelden van Vijfhoeken
- Het Pentagon-gebouw in Washington D.C., een van de grootste kantoorgebouwen ter wereld, dankt zijn naam aan zijn vijfhoekige vorm.
- De bloemblaadjes van een viooltje vormen een perfect voorbeeld van een vijfhoek in de natuur.
- Een voetbal is opgebouwd uit vijfhoeken en zeshoeken, die samen een stevige en ronde vorm creëren.
- Sommige verkeersborden hebben een vijfhoekige vorm, waardoor ze opvallen en de aandacht trekken.
- In de chemie komen vijfhoekige moleculen voor, zoals cyclopentaan.
Tips en Trucs voor het Werken met Vijfhoeken
- Gebruik een passer en een liniaal om nauwkeurige vijfhoeken te construeren.
- Bestudeer de eigenschappen van de gulden snede om de esthetische aantrekkingskracht van vijfhoeken beter te begrijpen.
- Zoek naar voorbeelden van vijfhoeken in je omgeving en probeer te analyseren waarom deze vorm is gekozen.
- Experimenteer met het tekenen en construeren van vijfhoeken om je ruimtelijk inzicht te verbeteren.
- Deel je kennis over vijfhoeken met anderen en laat je inspireren door hun ontdekkingen.
Vijfhoeken zijn meer dan alleen geometrische vormen. Ze zijn een weerspiegeling van de schoonheid en complexiteit van de wereld om ons heen. Van de kleinste bloemblaadjes tot de grootste bouwwerken, vijfhoeken blijven ons fascineren en inspireren. Door hun geheimen te ontrafelen, kunnen we niet alleen onze kennis van wiskunde en geometrie verdiepen, maar ook onze waardering voor de wonderen van de natuur en de menselijke creativiteit vergroten. Neem de tijd om de vijfhoeken om je heen te observeren, te bestuderen en te waarderen, en ontdek de verborgen schoonheid die deze fascinerende vorm te bieden heeft.
Veilig online zo kies je het beste internetfilter voor je kind
Gerard van der ven een diepgaande verkenning
De betoverende wereld van s werelds duurste jurken
