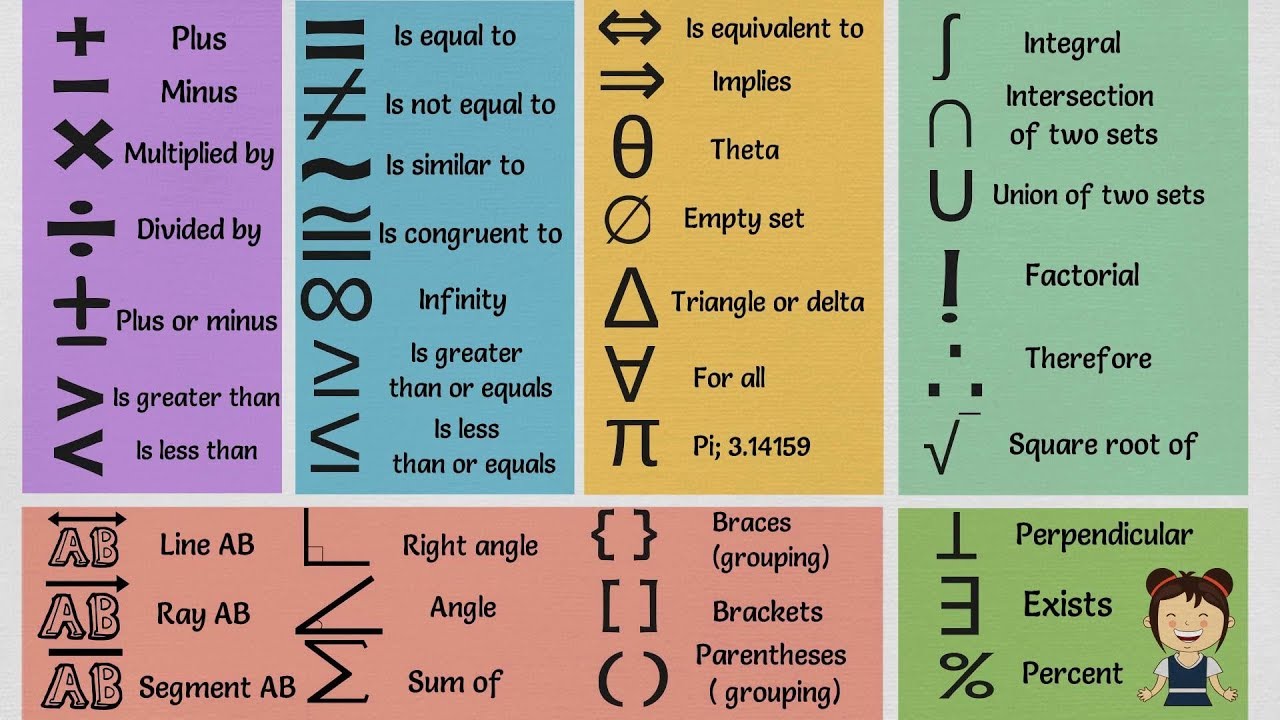
De mysterieuze 'd' in wiskundige formules ontrafeld

Rhonda 10 Jul 2024

Wat betekent die mysterieuze 'd' toch in wiskundige formules? Je hebt het vast wel eens gezien: d/dx, dy/dt, ∫f(x) dx. Die 'd' lijkt overal op te duiken, maar wat betekent het nu precies? Dit artikel duikt in de wereld van de 'd' en ontrafelt de geheimen achter deze belangrijke wiskundige notatie.

De 'd' in wiskundige formules staat vaak voor een infinitesimaal kleine verandering. Denk aan een oneindig kleine stap, een minuscule verandering in een variabele. Het is een concept dat centraal staat in de calculus, de tak van wiskunde die zich bezighoudt met verandering. Door deze infinitesimaal kleine veranderingen te bestuderen, kunnen we de helling van een curve bepalen, de oppervlakte onder een grafiek berekenen en nog veel meer.

De notatie 'd/dx' staat voor de afgeleide van een functie naar x. Het geeft de mate van verandering van de functie ten opzichte van x weer. Stel je voor dat je de snelheid van een auto wilt berekenen. De snelheid is de verandering in afstand over een bepaalde tijd. In wiskundige termen is dit de afgeleide van de afstand naar de tijd.

'dy/dt' vertegenwoordigt de afgeleide van y naar t. Dit wordt vaak gebruikt in de natuurkunde om de verandering van een grootheid in de tijd te beschrijven, zoals de snelheid (verandering in positie over tijd) of de versnelling (verandering in snelheid over tijd). Het begrijpen van deze notatie is cruciaal voor het begrijpen van dynamische systemen.

De 'd' verschijnt ook in integralen, zoals ∫f(x) dx. Hier staat de 'dx' voor een infinitesimaal kleine verandering in x. De integraal berekent de oppervlakte onder de grafiek van de functie f(x). Door de oppervlakte van oneindig dunne rechthoeken onder de curve op te tellen, krijgen we de totale oppervlakte.

De 'd' in de wiskunde heeft dus een rijke geschiedenis en is onlosmakelijk verbonden met de ontwikkeling van de calculus. Het concept van infinitesimaal kleine veranderingen was revolutionair en opende de deur naar een nieuw begrip van verandering en beweging.

Een belangrijk probleem bij het werken met infinitesimaal kleine veranderingen is het correct interpreteren ervan. Het zijn geen 'gewone' getallen, maar abstracte concepten die zorgvuldig moeten worden behandeld.

Voordelen van het gebruik van 'd' in calculus:

1. Concise notatie: Het maakt complexe concepten compact en leesbaar.

2. Universele taal: Het is een universeel begrepen symbool in de wiskunde.

3. Basis voor geavanceerde wiskunde: Het vormt de basis voor differentiaalvergelijkingen, vectorcalculus en andere geavanceerde wiskundige disciplines.

Veelgestelde vragen:

1. Wat betekent 'd' in d/dx? Antwoord: De afgeleide naar x.

2. Wat betekent 'dx' in een integraal? Antwoord: Een infinitesimaal kleine verandering in x.

3. Wie introduceerde de 'd' notatie? Antwoord: Leibniz.

4. Wat is het verschil tussen 'Δx' en 'dx'? Antwoord: Δx is een eindige verandering, dx is infinitesimaal klein.

5. Kan 'd' voor andere variabelen dan x en y staan? Antwoord: Ja, 'd' kan voor elke variabele staan.

6. Wat is de relatie tussen 'd' en de helling van een curve? Antwoord: De afgeleide (d/dx) geeft de helling van de raaklijn aan de curve weer.

7. Hoe wordt 'd' gebruikt in differentiaalvergelijkingen? Antwoord: Om de relatie tussen een functie en zijn afgeleiden te beschrijven.

8. Waar kan ik meer leren over 'd' in calculus? Antwoord: Calculus textbooks, online resources.

Conclusie: De 'd' in wiskundige formules, hoewel ogenschijnlijk klein, speelt een cruciale rol in ons begrip van verandering en beweging. Het is een krachtig symbool dat de basis vormt voor de calculus en vele andere gebieden van de wiskunde en natuurkunde. Door de betekenis en het gebruik ervan te begrijpen, kunnen we de complexiteit van de wereld om ons heen beter doorgronden. Duik dieper in de wereld van de calculus en ontdek de fascinerende mogelijkheden die de 'd' te bieden heeft. Het is een reis die je wiskundige horizon zeker zal verbreden.

De magie van 7 letter woorden beginnend met uni
Elektrische voertuigen presentatie de toekomst van mobiliteit
Gezamenlijk formularium zuid devon efficiente gezondheidszorg